Blue whales are the largest animals known to have lived on earth, and they can be seen right off the coast
of California! Just how big are they? Could a blue whale fit in your school yard? Start by asking students
what they know about blue whales. There are many options for learning about the whales, and you can have
students do research ahead of time, or share information from some of the resource links at the end of this
activity before heading out to the school yard.
Come prepared with a piece of rope that has been pre-measured to 100 feet (or 30 meters), or a long measuring
tape. Have two students each take one end of the rope and walk slowly apart until the rope is taut, then place
it on the ground. Explain that this is 100 feet and a blue whale can grow to this size. Have students line up
along the rope with their arms outstretched, fingertips just touching. Are they as big as the whale? Have students
close their eyes and imagine an animal as big as a blue whale, swimming next to them. What do they think it is
like to be a creature that size?
Older students can compare the length of a blue whale to the height of the tallest tree on their school grounds.
(They could also compare it to a flag pole, their school building, or other tall feature.) How tall do the
students think the tree is? One method to calculate the height is to compare shadows on a sunny day. Use
measuring tape to measure the shadow cast by the tree. Next measure a shadow cast by a yard stick (or meter stick)
held perpendicular to the ground.
How can we use ratios to determine the unknown value (the height of the tree)?
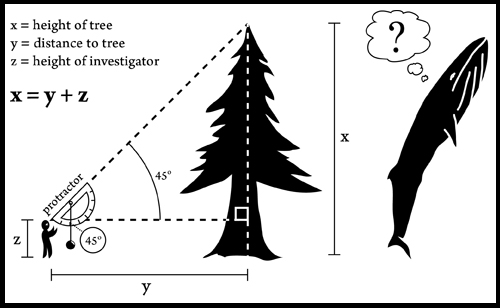Another method to calculate the height is to use a clinometer. Tape a straw or a small roll of paper to the
flat side of a protractor. Thread some string through the hole in the protractor (should be near the center of
the straw), and tie a weight (can be a paperclip or a washer) to the string so that it stretches past the bottom
of the protractor and can swing freely. Have one student look through the straw to see the top of the tree.
Have the student move farther from or closer to the tree until a partner tells them that the string is hanging
down at a 45 (or 135) degree angle on the protractor. The student has now formed an isosceles right triangle
with the tree. The distance from the student to the tree, plus the student's height, equals the height of the
tree. Is the tree taller than a blue whale is long? Can the students picture a blue whale next to the tree?
How many trees would it take to equal the length of the blue whale? Why might it be useful to be able to measure
a tree this way?
Further Resources:
